Métodos numéricos para EDPs

Nessa seção, desenvolveremos métodos de aproximação numérica para Equações Diferenciais Parciais. Para detalhes sobre os tipos de equações, consulte esse link.

Equações Elípticas

Considere a equação de Poisson $$\nabla^2 u(x,y) := u_{xx}(x,y) + u_{yy}(x,y) = f(x,y)$$ definida em um conjunto $U$ tal que $u(x,y) = g(x,y)$ em $(x,y)$ na fronteira de $U$. Em geral, tomamos $U = \{(x,y) \mid a < x < b, c < y < d\}$.

O método consiste na aplicação do método das Diferenças Finitas em um grid de duas dimensões. Seja $h = (b-a)/n$ e $k = (d-c)/m$ o tamanho do passo, em que $n$ e $m$ indicam a quantidade deles em cada direção. A representação do desenho foi retirada de https://sites.me.ucsb.edu/~moehlis/APC591/tutorials/tutorial5/node3.html e segue abaixo:

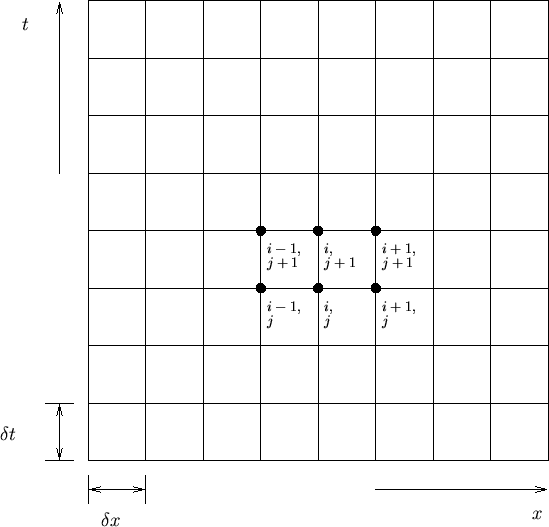
Nessa imagem $\delta x = h$ e $\delta t = k$. Com o grid, obtemos que $x_i = a + ih$ e $y_j = c + jk$, para $i, j = 0, \dots, m$. Usando a expansão de Taylor na variável $x$ e $y$, geramos a fórmula de diferenças centrada $$\frac{\partial ^2 u}{\partial x^2}u(x_i, y_j) = \frac{u(x_{i+1}, y_j) - 2u(x_{i}, y_j) + u(x_{i-1}, y_j)}{h^2} - \frac{h^2}{12}\frac{\partial^4 u}{\partial x^4}(\xi_i, y_j),$$ em que $\xi_i \in (x_{i-1}, x_{i+1})$, e $$\frac{\partial ^2 u}{\partial y^2}u(x_i, y_j) = \frac{u(x_{i}, y_{j+1}) - 2u(x_{i}, y_j) + u(x_{i}, y_{j-1})}{k^2} - \frac{k^2}{12}\frac{\partial^4 u}{\partial y^4}(x_i, \eta_j),$$ em que $\eta_i \in (y_{i-1}, y_{i+1})$. Aplicando na equação de Poisson, $$\frac{u(x_{i+1}, y_j) - 2u(x_{i}, y_j) + u(x_{i-1}, y_j)}{h^2} + \frac{u(x_{i}, y_{j+1}) - 2u(x_{i}, y_j) + u(x_{i}, y_{j-1})}{k^2} = f(x_i, y_j) + \frac{h^2}{12}\frac{\partial^4 u}{\partial x^4}(\xi_i, y_j) + \frac{k^2}{12}\frac{\partial^4 u}{\partial y^4}(x_i, \eta_j),$$ com as restrições de contorno. Usando a notação $w_{ij} \approx u(x_{i}, y_j)$, multiplicando ambos os lados pro $h^2$ e juntando os termos, obtemos que $$2\left[\left(\frac{h}{k}\right)^2 + 1\right]w_{ij} - (w_{i+1,j} + w_{i-1,j})- \left(\frac{h}{k}\right)^2(w_{i,j+1} + w_{i,j-1}) = -h^2f(x_i, y_j),$$ que tem erro local de ordem $h^2 + k^2$. Note que isso formará um sistema de equações com variáveis desconhecidas $w_{ij}$. É usual denotar $$w_l = w_{ij}, l = i + (m-1-j)(n-1)$$ para $i = 1,2, \dots, n-1$ e $j=1,2,\dots,m-1$.

Equações Parabólicas

A primeira equação é a do calor ou difusão, dada por $$\frac{\partial u}{\partial t} = \frac{\partial^2 u}{\partial x^2},$$ com condições $$u(x,0) = f(x), u(0,t) = a(t), \text{ e } u(1,t) = b(t).$$

Usando a Fórmula de Taylor mais uma vez e a aproximação $w_{ij} \approx u(x_i, y_j)$, obtemos que $$\frac{w_{i, j+1} - w_{ij}}{k} - \alpha^2 \frac{w_{i+1,j} - 2w_{ij} + w_{i-1,j}}{h^2} = 0,$$ que pode ser reescrito como $$w_{i,j+1} = \left(1 - \frac{2\alpha^2 k }{h^2}\right)w_{ij} + \alpha^2 \frac{k}{h^2}(w_{i+1,j} + w_{i-1,j})$$ para $i=1,2, \dots, m-1$ e $j=1,2,\dots$. Além, disso temos os valores de contorno, $w_{i0} = f(x_i)$ para $i= 0, 1, \dots, m, w_{m j} = b(kj), \text{ and } w_{0 j} = a(kj)$.

Esse método de atualização é conhecido como Forward-Difference e o método tem erro local de ordem $O(k + h^2)$. Note que a atualização pode ser escrita em formato matricial: $w^{(j)} = Aw^{(j-1)}$, em que $w^{(j)} = (w_{1j}, \dots, w_{mj})$.

Estabilidade

Suponha que o valor inicial $w^{(0)}$ seja representado com erro numérico $e^{(0)}$. Esse erro vai se propagar pelas iterações, dado que $$w^{(1)} = Aw^{(0)} + Ae^{(0)}, \quad w^{(2)} = A^2w^{(0)} + A^2e^{(0)}, \quad w^{(3)} = A^3w^{(0)} + A^3e^{(0)},$$ e assim por diante. Isso significa que não queremos que $||A^n e^{(0)}||$ cresça com $n$. Isso acontece se para qualquer erro, $$||A^ne^{(0)}|| \le ||e^{(0)}||, \text{ for all } n.$$ Com isso, gostaríamos que $||A^n|| \le 1$ e, por conseguinte, $\rho(A) \le 1$. Essa restrição implica na condição de estabilidade para esse método: $$\alpha^2 \frac{k}{h^2} \le \frac{1}{2}.$$

Backward-Difference

Nesse método, usamos que $$\frac{\partial u}{\partial t}(x_i, t_j) = \frac{u(x_i, t_j) - u(x_i, t_{j-1}}{k} + \frac{k}{2}\frac{\partial ^2 u}{\partial t^2}(x_i, \mu_j).$$

Assim, chegamos na fórmula de atualização

$$\frac{w_{i, j} - w_{i,j-1}}{k} - \alpha^2 \frac{w_{i+1,j} - 2w_{ij} + w_{i-1,j}}{h^2} = 0$$

Denote $\lambda = \alpha^2(k/h^2)$. Então o método vira $$(1+2\lambda)w_{ij} - \lambda w_{i+1, j} - \lambda w_{i-1,j} = w_{i, j-1}$$

Note que nesse caso, teremos que $Aw^{(j)} = w^{(j-1)}.$ Podemos verificar que quando $\lambda > 0$, a matriz é $A$ é estritamente diagonalmente dominante e positiva definida. Um Solver de sistema linear deve ser utilizado para encontrar o próximo passo $w^{(j)}$. Uma análise nos autovalores de $A$ prova que o método backward é estável incondicionalmente.

Além dela, ainda temos a fórmula Centered-Difference que diz que $$\frac{w_{i,j+1} - w_{i,j-1}}{2k} = \alpha^2\frac{w_{i+1,j} - 2w_{ij} + w_{i-1, j}}{h^2}.$$ Esse método tem a vantagem de ter erro local $O(h^2 + k^2)$, mas tem problemas de estabilidade como o Forward.

Crank-Nicolson

A ideia desse método é tomar a média dos passo $j$ do método Forward e do passo $j+1$ do método Backward, dados por

$$\frac{w_{i, j+1} - w_{i,j}}{k} - \alpha^2 \frac{w_{i+1,j} - 2w_{ij} + w_{i-1,j}}{h^2} = 0$$ e $$\frac{w_{i, j+1} - w_{i,j-1}}{k} - \alpha^2 \frac{w_{i+1,j+1} - 2w_{i,j+1} + w_{i-1,j+1}}{h^2} = 0$$ que leva a $$\frac{w_{i, j+1} - w_{i,j}}{k} - \frac{\alpha^2}{2}\left[\frac{w_{i+1,j} - 2w_{ij} + w_{i-1,j}}{h^2} + \frac{w_{i+1,j+1} - 2w_{i,j+1} + w_{i-1,j+1}}{h^2}\right] = 0.$$ Esse método tem erro local $O(k^2 + h^2)$. Em forma matricial, esse método é da forma $Aw^{(j+1)} = Bw^{(j)}$. É fácil verificar que $A$ é positiva definida com diagonal estritamente dominante. Além disso, o método é incondicionalmente estável.

Equações Hiperbólicas

O principal exemplo desse tipo de equação é a equação da onda que é dada por $u_{tt}(x,t) = \alpha^2 u_{xx}(x,t)$ com condições iniciais e finais $u(x,0) = f(x), u_t(x,0) = g(x), u(0,t) = p(t), u(l,t) = q(t)$, em que $0 < x < l$. As ideias do grid e da aproximação de Taylor são as mesmas, o que leva ao método das diferenças $$\frac{w_{i,j+1} - 2w_{ij} + w_{i,j-1}}{k^2} - \alpha^2\frac{w_{i+1,j} - 2w_{ij} + w_{i-1, j}}{h^2} = 0.$$ Ponha $\lambda = \alpha k / h$. Então reescrevemos a equação acima como $$w_{i,j+1} = 2(1 - \lambda^2)w_{i,j} + \lambda^2(w_{i+1,j} + w_{i-1,j}) -w_{i,j-1}.$$ Note que para o passo $j+1$ são necessários conhecer dois passos anteriores. Para calcular $w_{i2}$ precisamos saber $w_{i0} = f(x_i)$ e $w_{i1}$. Esse último valor vai ser aproximado usando a condição inicial da derivada $g(x)$, obtida através de $$w_{i,1} = w_{i,0} + kg(x_i).$$ Também podemos melhor essa aproximação de Euler usando o polinômio de Maclaurin em $t$: $$w_{i,1} = w_{i,0} + kg(x_i) + \frac{\alpha^2 k^2}{2}f''(x_i),$$ que tem erro de aproximação $O(k^3)$. Esse método é estável se $\lambda \le 1$.