Histogram Matching

Também conhecido como Histogram Specification. Quando utilizamos o método anterior para equalizar o histograma, vimos que isso pode ser automatizado, produzindo uma imagem com histograma uniforme (Basta fazer o cálculo de \(p_s(s)\)). Entretanto, às vezes é interessante especificar a forma do histograma que desejamos que a imagem processada tenha. Aplica-se para fazer o match entre imagens de dois sensores, cuja resposta seja levemente diferente. Assim, consideremos \(p_r(r)\) e \(p_z(z)\) PDFs, que representam a distribuição do histrograma, da imagem original e da imagem processada, respectivamente. Tomemos, então \(s\) de forma que \(s = T(r) = \int_0^r p_r(w) dw \) e definamos \(z\) com a propriedade \(G(z) = \int_0^z p_z(t) dt = s\). Desta dorma, \(G(z) = T(r) \implies z = G^{-1}[T(r)]\), assumindo a existência da inversa de \(G\). Desta forma:

1. Obtenho as distribuições acumuladas \(T(r) \) e \(G(z)\) como anteriormente;
2. Obtenho a transformação \(G^{-1}\), fazendo a comparação das distribuições (Veja imagem abaixo); e
3. Obtenho a imagem de saída.

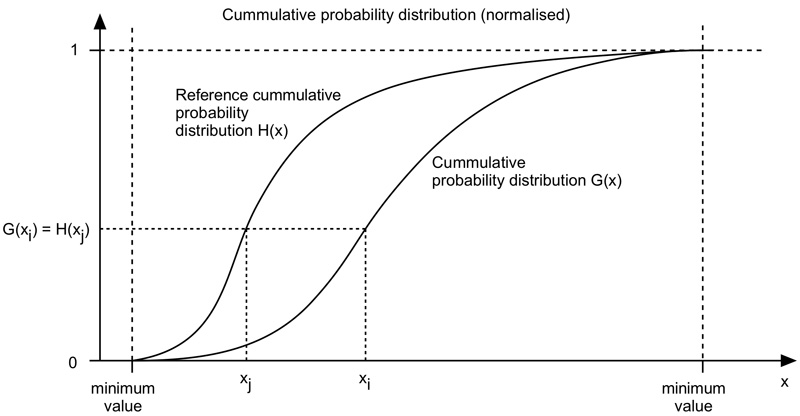
Todavia, obter essas expressões analitícamente nem sempre é possível. Em contrapartida, podemos utilizar no caso discreto com algumas aproximações. Essas aproximações funcionam como uma comparação de elemento a elemento para cada tom diferente, buscando uma aproximação para o tom mais próximo. Façamos um primeiro exemplo com a imagem crítica descrita acima. Usaremos, como referência a distribuição do histograma da primeira imagem, pois ela deixa bem visível a célula. Outro motivo que a função \(G\) é injetiva no grande espectro, visto que \(p_z(z) > 0\), para quase todo \(z\).

A diferença é notável. Porém, algo incomoda o modelo para mim: A área de preto, que agora se tornou cinza. Esse dado é dado perdido. Atualize até 10 vezes, caso a tela fique preta.

Para a equalização de histograma e para o histogram matching, desenvolvi na linguagem de programação Python um arquivo com uma classe que implementa o que necessito para ter essas funções. Chamei essa classe de HistogramEqualization. A partir dela, é mais fácil fazer a equalização de histogramas de imagens de forma estruturada.

Testando com Distribuição Beta

Às vezes, não queremos utilizar uma imagem do nosso domínio de imagens para fazer o matching de histograma, pois as imagens podem todas ter uma densidade conjunta não necessariamente monótona estritamente crescente, para assim, poder utilizar o método acima citado. Neste caso, a distribuição beta tem duas propriedades desejadas para o estudo em questão: flexibilidade, devido à escolha de dois parâmetros, que permite observar diferentes curvas; e ela tem o suporte no intervalo \([0,1]\), limitado, como o nosso modelo em questão. Desta maneira, basta discretizar esse intervalo de maneira uniforme e aumentá-lo linearmente para o intervalo \([0,255]\) e utilizar a distribuição beta.

O problema passa, então, para um problema matemático, com diferentes interpretações: uma visão do problema pode ser com otimização. Imagine que eu tome cada imagem do meu banco de dados, e calcule a distribuição conjunta. Agora, poderia interpretar o problema como: \(\min_{\alpha,\beta} \sum_{i=1}^N \sum_{j = 0}^{255} \min_{k} |G_{\alpha,\beta}(k) - T_i(j)|\), onde \(T:[0,255] \to [0,1]\) é a função acumulada da imagem, \(G:[0,255] \to [0,1]\) é a função da distribuição acumulada da função beta, \(\alpha, \beta\) são os parâmetros da distribuição e \(N\) é o número de imagens. Note que, a grosso modo essa modelagem permite, dado uma distribuição beta, eu somo os erros de cada tom, minimizando eles sempre. Outra forma de imaginar o problema é enxergar como um problema estatístico, onde queremos estimar \(\alpha, \beta\), parâmetros da minha distribuição.

Antes de dar um pouco de carga matemática nesse problema, eu pretendo neste trabalho observar qualitativamente a relação dessas distribuições com o resultado das imagens. Neste caso, como vou tratar de problemas um tanto mais específicos e que existem um pouco mais de cálculo por causa da distribuição beta, a linguagem javascript fica mais restrita e não é boa para o caso. Nesse sentido, pretendo a utilizar a linguagem Python para mostrar a diferença nesses modelos. Observe, assim, algumas imagens geradas pelas diferentes distribuições, sujeitas a \(\alpha, \beta\). Para fazer os testes, recomendo usar o arquivo "image.py" que se encontra no GitHub de Lucas Moschen, como constado nas referências. Nele é possível alterar os parâmetros e obter as mais variadas imagens.

Uma outra forma de obter um resultado similar é primeiro fazer a equalização de histograma em uma das imagens e depois utilizá-la como referência. O que acredito ser interessante é que variando apenas dois parâmetros, posso obter as mais variadas imagens extremamente distintas, como pudemos observar.

Demonstração do Histogram Matching

Este algoritmo tem o objetivo de modificar uma imagem de forma a seu histograma corresponder a um outro histograma, em geral da mesma base dados. Ele é de simples implementação. Nessa representação, permito o usuário escolher dos parâmtetros, \(\alpha > 0\) e \(\beta > 0\) da distribuição beta, para podermos ter uma referência. Não preciso montar uma ilustração para o algoritmo de Equalização de Histogramas, pois ele é um subitem do Histogram Matching da distribuição uniforme, que nesse caso, é a distribuição \(Beta(1,1)\).